Parallel lines and congruent angles make corresponding angles in both triangles equal. One side (half of median) and two angles equal, so triangles congruent (AAS). QED (29 words).
Sure, I can help you with this geometry problem. The givens are that $
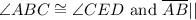
 $. You need to prove that
$. You need to prove that
 .
.
I can see that you have already started working on the proof. You have written down the first three statements and reasons:
1.
 (Given)
(Given)
2.
 (Given)
(Given)
3.
 (Vertical angles)
(Vertical angles)
The next step is to use these statements to prove that one of the side pairs of the triangles is congruent. Once you have proven that one pair of sides is congruent, you can use the Angle-Angle-Side (AAS) congruence criterion to prove that the triangles are congruent.
Here are two possible approaches you could take:
Approach 1:Use the fact that
 is a median of
is a median of
 to prove that
to prove that

4.
 is the midpoint of
is the midpoint of
 (Given)
(Given)
5.
 is a median of
is a median of
 (Definition of a median)
(Definition of a median)
6.
 (Property of a median)
(Property of a median)
Approach 2: Use the fact that
 is a transversal to parallel lines
is a transversal to parallel lines
 and
and
 to prove that
to prove that


4.
 is a transversal to
is a transversal to
 and
and
 (Given)
(Given)
5.
 (Alternate interior angles)
(Alternate interior angles)
Once you have proven that one pair of sides is congruent and one pair of angles is congruent, you can use the AAS congruence criterion to conclude that
