Question

What is an equation of the line that passes through the points left bracket, 8, comma, minus, 3, right bracket(8,−3) and left bracket, 4, comma, 2, right bracket(4,2)?

Answer 1

The equation of the line passing through the points (8, -3) and (4, 2) is y=− 5/2x+7.

To find the equation of the line passing through the points (8, -3) and (4, 2), we can use the slope-intercept form of a linear equation, which is y=mx+b, where m is the slope and b is the y-intercept.

First, calculate the slope (m) using the formula

m=
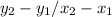`y_2-y_1/x_2-x_1`, where (x1​,y1​) and (x2​,y2 ) are the coordinates of the two points.

m= 2−(−3)/4−8= 5/−4

Now that we have the slope, choose one of the points (let's use (8, -3)) to substitute into the equation. The slope-intercept form becomes

y=− 5/4x+b.

Substitute the coordinates of the point (8, -3) into the equation to solve for b:

−3=− 5/4×8+b

−3=−10+b

b=7

Now that we have the slope (−5/4) and the y-intercept (b=7), the equation of the line is y=− 5/4x+7. Therefore, the line passing through the points (8, -3) and (4, 2) can be represented by this equation.