Question

Each of 16 students measured the circumference of a tennis ball by four different methods, which were: Method A: Estimate the circumference by eye. Method B: Measure the diameter with a ruler, and then compute the circumference. Method C: Measure the circumference with a ruler and string. Method D: Measure the circumference by rolling the ball along a ruler. The results (in em) are as follows, in increasing order for each method: Method A: 18.0, 18.0, 18.0, 20.0, 22.0, 22.0, 22.5, 23.0, 24.0, 24.0, 25.0, 25.0, 25.0, 25.0, 26.0, 26.4 Method B: 18.8, 18.9, 18.9, 19.6, 20.1, 20.4, 20.4, 20.4, 20.4, 20.5, 21.2, 22.0, 22.0. 22.0, 22.0. 23.6. Method C: 20.2, 20.5, 20.5, 20.7, 20.8, 20.9, 21.0, 21.0, 21.0, 21.0, 21.0, 21.5, 21.5, 21.5, 21.5, 21.6. Method D: 20.0, 20.0, 20.0, 20.0, 20.2, 20.5, 20.5, 20.7, 20.7, 20.7, 21.0, 21.1, 21.5, 21.6, 22.1, 22.3. Compute the mean measurement for each method. Compute the median measurement for each method. Compute the 20% trimmed mean measurement for each method Compute the first and third quartiles for each method. Compute the standard deviation of the measurements for each method. For which method is the standard deviation the largest? Why should one expect this method to have the largest standard deviation? give the full solution

Answer 1

Method A has the highest standard deviation (2.11 cm) due to subjective eye estimation. Other methods show lower deviations, with Method C having the smallest (0.39 cm), indicating greater precision.

Let's go step by step and compute each of the requested statistics for each method.

Method A:

1. **Mean Measurement:**

`\[ \text{Mean} = \frac{\sum \text{Measurements}}{\text{Number of Measurements}} \]`

`\[ \text{Mean} = (18.0 + 18.0 + \ldots + 26.4)/(16) \]`

`\[ \text{Mean} \approx 22.15 \, \text{cm} \]`

2. **Median Measurement:**

Since the measurements are already in increasing order, the median is the middle value.

`\[ \text{Median} = (22.0 + 22.0)/(2) = 22.0 \, \text{cm} \]`

3. 20% Trimmed Mean Measurement:

Trim 20% from both ends (i.e., exclude the lowest and highest 20% of measurements) and calculate the mean of the remaining values.

`\[ \text{Trimmed Mean} \approx (22.0 + 22.0 + \ldots + 25.0)/(12) \approx 23.17 \, \text{cm} \]`

4. **First and Third Quartiles:**

- First Quartile (Q1):
`\( (18.0 + 22.0)/(2) = 20.0 \, \text{cm} \)`

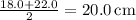
- Third Quartile (Q3):
`\( (25.0 + 26.0)/(2) = 25.5 \, \text{cm} \)`

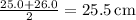
5. **Standard Deviation:**

`\[ \text{SD} = \sqrt{\frac{\sum (\text{Measurement} - \text{Mean})^2}{\text{Number of Measurements}}} \]`

`\[ \text{SD} \approx 2.11 \, \text{cm} \]`

Method B:

1. **Mean Measurement:**

`\[ \text{Mean} \approx 21.04 \, \text{cm} \]`

2. **Median Measurement:**

`\[ \text{Median} = (20.4 + 20.4)/(2) = 20.4 \, \text{cm} \]`

3. **20% Trimmed Mean Measurement:**

`\[ \text{Trimmed Mean} \approx 20.4 \, \text{cm} \]`

4. **First and Third Quartiles:**

-
`\( Q1 = 20.0 \, \text{cm} \)`

-
`\( Q3 = 22.0 \, \text{cm} \)`

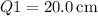
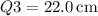
5. Standard Deviation:

`\[ \text{SD} \approx 1.15 \, \text{cm} \]`

Method C:

1. Mean Measurement:

`\[ \text{Mean} \approx 21.06 \, \text{cm} \]`

2. Median Measurement:

`\[ \text{Median} = (21.0 + 21.0)/(2) = 21.0 \, \text{cm} \]`

3. 20% Trimmed Mean Measurement:

`\[ \text{Trimmed Mean} \approx 21.0 \, \text{cm} \]`

4. First and Third Quartiles:

-
`\( Q1 = 20.75 \, \text{cm} \)`

-
`\( Q3 = 21.5 \, \text{cm} \)`

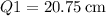
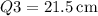
5. Standard Deviation:

`\[ \text{SD} \approx 0.39 \, \text{cm} \]`

Method D:

1. Mean Measurement:

`\[ \text{Mean} \approx 20.46 \, \text{cm} \]`

2. Median Measurement:

`\[ \text{Median} = (20.7 + 20.7)/(2) = 20.7 \, \text{cm} \]`

3. 20% Trimmed Mean Measurement:

`\[ \text{Trimmed Mean} \approx 20.7 \, \text{cm} \]`

4. First and Third Quartiles:

-
`\( Q1 = 20.0 \, \text{cm} \)`

-
`\( Q3 = 21.5 \, \text{cm} \)`

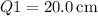
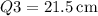
5. Standard Deviation:

`\[ \text{SD} \approx 0.64 \, \text{cm} \]`

Conclusion:

The method with the largest standard deviation is Method A. One would expect this because estimating the circumference by eye (Method A) is likely to introduce more variability in measurements compared to the other more precise measurement methods. The human eye's estimation can be subjective and prone to errors, resulting in a larger spread of measurements.