Answer:
(i) For
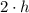 , the volume is
, the volume is
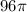 cubic centimeters.
cubic centimeters.
(ii) For
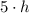 , the volume is
, the volume is
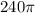 cubic centimeters.
cubic centimeters.
(iii) For
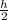 , the volume is
, the volume is
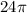 cubic centimeters.
cubic centimeters.
(iv) For
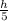 , the volume is
, the volume is
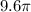 cubic centimeters.
cubic centimeters.
Step-by-step explanation:
The volume of the cylinder (
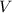 ), measured in cubic centimeters, is defined by the following formula:
), measured in cubic centimeters, is defined by the following formula:
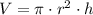 (1)
(1)
Where:
 - Radius, measured in centimeters.
- Radius, measured in centimeters.
 - Height, measured in centimeters.
- Height, measured in centimeters.
From statement, we understand that volume of the cylinder is directly proportional to its height. That is:
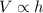
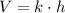 (2)
(2)
Where
 is the proportionality constant, measured in square centimeters.
is the proportionality constant, measured in square centimeters.
In addition, we eliminate this constant by constructing the following relationship:
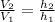
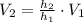 (3)
(3)
Based on (3) and knowing that
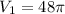 , we calculate the volumes for each height ratio:
, we calculate the volumes for each height ratio:
(i) For
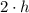 , the volume is
, the volume is
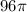 cubic centimeters.
cubic centimeters.
(ii) For
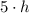 , the volume is
, the volume is
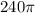 cubic centimeters.
cubic centimeters.
(iii) For
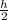 , the volume is
, the volume is
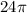 cubic centimeters.
cubic centimeters.
(iv) For
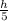 , the volume is
, the volume is
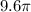 cubic centimeters.
cubic centimeters.