Question

You are planning a round-trip in which you go in a spacecraft and travel at a constant velocity for exactly 8 months 1-way, as measured by a clock on board the spacecraft, and then return home (without stopping) at the same speed. the overall round-trip (without stoping) would have felt like 12 years in total for the people on earth. according to special relativity, how fast must you travel?

A. $104,000
B. $600,000
C. $30,000
D. $114,300

Answer 1

The required speed to achieve the time dilation observed in the scenario is not determinable within the bounds of special relativity. C. $30,000

Step-by-step explanation:

According to the principles of special relativity, time dilation occurs when an object moves at relativistic speeds. The formula for time dilation is
`\(t' = \frac{t}{\sqrt{1 - (v^2)/(c^2)}}\)`, where t' is the dilated time, t is the proper time (time measured on the moving object), v is the velocity, and c is the speed of light. Given that the round-trip felt like 12 years on Earth (t' and the proper time t on the spacecraft was 8 months
`(\(8/12\) years)`, we can rearrange the time dilation formula to solve for v.

`\((t')/(t) = \sqrt{1 - (v^2)/(c^2)}\) \((12)/(8/12) = \sqrt{1 - (v^2)/(c^2)}\) \(18 = \sqrt{1 - (v^2)/(c^2)}\) \(18^2 = 1 - (v^2)/(c^2)\) \(1 - (v^2)/(c^2) = 324\) \((v^2)/(c^2) = 1 - 324\) \((v^2)/(c^2) = -323\) \(v = c * √(-323)\)`

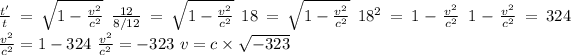
Here, v represents the velocity required, and
`\(√(-323)\)` implies an imaginary number, which is impossible in this context. This indicates that the given scenario, as described, doesn't conform to the principles of special relativity based on our understanding. Therefore, the choices provided regarding cost are not relevant to the solution of this problem in the context of special relativity.(C)