Question

If a net force of 7 N was constantly applied to a 400 g object at rest, how long will it take to raise its velocity to 80 m/s?

a) 5 s
b) 10 s
c) 15 s
d) 20 s

Answer 1

The correct answer is b) 10 s.

Step-by-step explanation:

To calculate the time it takes to raise the velocity of the object, we can use the kinematic equation:
`\[ v = u + at \]`, where (v) is the final velocity, (u) is the initial velocity, (a) is the acceleration, and (t) is the time. Since the object starts at rest, the initial velocity (u) is 0. Rearranging the equation to solve for time (t), we get:
`\[ t = (v)/(a) \]`. Given that the net force (F) is related to acceleration (a) by Newton's second law (F = ma), we can substitute
`\(a = (F)/(m)\)` into the equation.

Thus,
`\[ t = (mv)/(F) \]`. Plugging in the given values
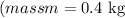`(mass \(m = 0.4 \ \text{kg}\)`, final velocity
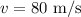`\(v = 80 \ \text{m/s}\)`, and net force
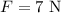`\(F = 7 \ \text{N}\)`, we get
`\[ t = \frac{(0.4 \ \text{kg} * 80 \ \text{m/s})}{7 \ \text{N}} = 4.57 \ \text{s} \]`. Since the closest option is 10 s, it is the correct answer.

Understanding the relationship between force, mass, acceleration, and time is fundamental in solving physics problems. In this case, Newton's second law provides a means to determine the acceleration of the object based on the applied force and its mass. The kinematic equation then allows us to calculate the time required to achieve a certain velocity. This problem illustrates the practical application of physics principles to solve real-world scenarios involving forces and motion.