Question

1

2
O
3
(10)
4
O (3.00)
O (-0,3)
0 (-00, +00)
5
6
7
8
If u(x) = -2x²+3 and v(x)= =, what is the range of (uv)(x)?
X
9
10

Answer 1

The range of (uv)(x) is D. (−∞,+∞) or in interval notation, (−∞,+∞).

The product of two functions u(x) and v(x) is denoted as (uv)(x) or u(x)×v(x).

Given:

u(x)=−
`2x^2 +3`

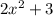
v(x)=
`(1)/(x)`

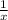
​Let's find (uv)(x):

(uv)(x)=u(x)×v(x)

(uv)(x)=
`(-2x^2+ 3) * (1)/(x)`

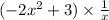
​Simplify this expression.

(uv)(x)=−2x+
`(3)/(x)`

​The range of (uv)(x) would depend on the values that x can take. As x approaches positive or negative infinity, −2x approaches negative or positive infinity respectively, while
`(3)/(x)` approaches 0.

So, as x approaches infinity, (uv)(x) approaches negative infinity, and as x approaches negative infinity, (uv)(x) approaches positive infinity.

Therefore, the range of (uv)(x) is (−∞,+∞) or in interval notation, (−∞,+∞).

Question

If u(x)=-2x²+3 and V(x)= 1/x what is the range of (uv)(x)?

A. (3.0)

B. (3,0)

C. (-∞,3)

D. (-∞,+∞)