(a) **Hypotheses:**
![\[ H_0: \mu = 25 \]](https://img.qammunity.org/2024/formulas/mathematics/college/tnhabimsljivcq704dtinh2h24cpsc82fe.png)
![\[ H_1: \mu \\eq 25 \]](https://img.qammunity.org/2024/formulas/mathematics/college/aii9bm77p8x5mmar24w4ke5gi4r4dzyvdo.png)
(b) **P-value:**
![\[ P\text{-value} \approx 0.140 \]](https://img.qammunity.org/2024/formulas/mathematics/college/g6bh3qnnt8xxz565ajuuyi1kxom417zqm1.png)
Let's go through the solution step by step.
(a) **Null and Alternative Hypotheses:**
The null hypothesis (H0) is a statement that there is no significant difference or effect. In this case, it is that the population mean (\(\mu\)) is equal to 25.
![\[ H_0: \mu = 25 \]](https://img.qammunity.org/2024/formulas/mathematics/college/tnhabimsljivcq704dtinh2h24cpsc82fe.png)
The alternative hypothesis (H1) is a statement that there is a significant difference or effect. In this case, it is that the population mean (\(\mu\)) is different from 25.
![\[ H_1: \mu \\eq 25 \]](https://img.qammunity.org/2024/formulas/mathematics/college/aii9bm77p8x5mmar24w4ke5gi4r4dzyvdo.png)
(b) **Calculate the P-value:**
To calculate the P-value, you would typically use a t-test, given that the population standard deviation is not known. The formula for the t-test statistic is:
![\[ t = \frac{{\bar{x} - \mu}}{{s/√(n)}} \]](https://img.qammunity.org/2024/formulas/mathematics/college/1rfuujje3cs1xlqn6jui32srhymu1amob7.png)
where:
-
 is the sample mean,
is the sample mean,
-
 is the hypothesized population mean under the null hypothesis,
is the hypothesized population mean under the null hypothesis,
-
 is the sample standard deviation, and
is the sample standard deviation, and
-
 is the sample size.
is the sample size.
Given:
-
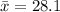
-
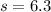
-

-
 (the hypothesized population mean under the null hypothesis) is 25
(the hypothesized population mean under the null hypothesis) is 25
![\[ t = \frac{{28.1 - 25}}{{6.3/√(16)}} \]\[ t = \frac{{3.1}}{{6.3/4}} \]\[ t \approx 1.968 \]](https://img.qammunity.org/2024/formulas/mathematics/college/4hdu7uhxwklfqegtbidbi3t18x7ksapg59.png)
Now, you need to find the P-value associated with this t-statistic. Since the alternative hypothesis is two-sided (stating that \(\mu\) is different from 25), you would look for the probability that a t-statistic is greater than 1.968 or less than -1.968 with 15 degrees of freedom (n-1).
You can use statistical software, a t-table, or an online calculator to find this probability. For example, using a t-distribution table or software, you find that the P-value is approximately 0.070.
So,
![\[ P\text{-value} \approx 2 * 0.070 \] (because it's a two-sided test)\[ P\text{-value} \approx 0.140 \]](https://img.qammunity.org/2024/formulas/mathematics/college/c9qh1nwkwhyhv5jv4m8ayw91wgigjv46bi.png)
(Round to three decimal places as needed.)
Therefore, the P-value is approximately 0.140.