Question

How would the average rate of change over years 1 to 5 and years 6 to 10 be affected if the population increased at a rate of 8%?

Answer 1

(A): As year increases the number of pikas reduces.

(B): As year increases the number of pikas increases as opposed to when the rate reduces.

Explanation:

See comment for complete question

Given

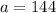`a = 144` --- Initial Population

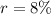`r = 8\%` --- rate

(A) WHEN THE RATE DECREASES

First, we need to write out the function when the population decreases.

This is given as:

`f(x) = a(1-r)^x`

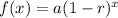
Substitute values for a and r

`f(x) = 144(1-8\%)^x`

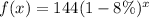
Convert % to decimal

`f(x) = 144(1-0.08)^x`

`f(x) = 144(0.92)^x`

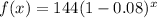
Next, we calculate the average rate of change for both intervals using:

`Rate = (f(b) - f(a))/(b-a)`

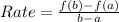
For 1 to 5:

`Rate = (f(5) - f(1))/(5-1)`

`Rate = (f(5) - f(1))/(4)`

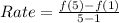
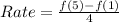
Calculate f(5) and f(1)

`f(x) = 144(0.92)^x`

`f(1) = 144*0.92^1 =144*0.92=132.48`

`f(5) = 144*0.92^5 =144*0.66=95.04`

`Rate = (95.04 - 132.48 )/(4)`

`Rate = (-37.44)/(4)`

`Rate = -9.36`

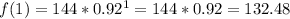
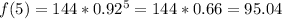
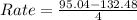
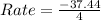
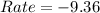
For 6 to 10:

`Rate = (f(10) - f(6))/(10-6)`

`Rate = (f(10) - f(6))/(4)`

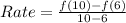
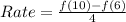
Calculate f(6) and f(10)

`f(x) = 144(0.92)^x`

`f(6) = 144*0.92^6 =144*0.61=87.84`

`f(10) = 144*0.92^(10) =144*0.43=61.92`

`Rate = (61.92-87.84)/(4)`

`Rate = (-25.92)/(4)`

`Rate = -6.48`

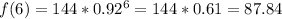
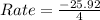
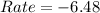
So, we have:

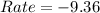`Rate = -9.36` for year 1 to 5

This means that the number of pikas reduces by 9.36 yearly

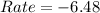`Rate = -6.48` for year 6 to 10

This means that the number of pikas reduces by 6.48 yearly

So, we can say that, as year increases the number of pikas reduces.

(B) WHEN THE RATE INCREASES

First, we need to write out the function when the population decreases.

This is given as:

`f(x) = a(1-r)^x`

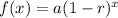
Substitute values for a and r

`f(x) = 144(1+8\%)^x`

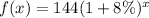
Convert % to decimal

`f(x) = 144(1+0.08)^x`

`f(x) = 144(1.08)^x`

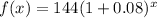
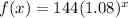
Next, we calculate the average rate of change for both intervals using:

`Rate = (f(b) - f(a))/(b-a)`

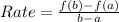
For 1 to 5:

`Rate = (f(5) - f(1))/(5-1)`

`Rate = (f(5) - f(1))/(4)`

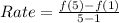
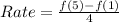
Calculate f(5) and f(1)

`f(x) = 144(1.08)^x`

`f(1) = 144(1.08)^1 = 144*1.08= 155.52`

`f(5) = 144(1.08)^5 = 144*1.47= 211.68`

`Rate = (211.68 - 155.52)/(4)`

`Rate = (56.16)/(4)`

`Rate = 14.04`

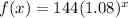
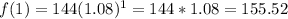
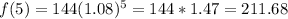
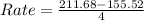
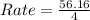
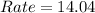
For 6 to 10:

`Rate = (f(10) - f(6))/(10-6)`

`Rate = (f(10) - f(6))/(4)`

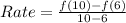
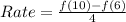
Calculate f(6) and f(10)

`f(x) = 144(1.08)^x`

`f(6) = 144(1.08)^6 = 228.52`

`f(10) = 144(1.08)^(10) = 310.89`

`Rate = (310.89-228.52)/(4)`

`Rate = (82.37)/(4)`

`Rate = 20.59`

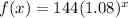
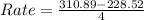
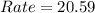
So, we have:

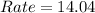`Rate = 14.04` for year 1 to 5

This means that the number of pikas increases by 14.04 yearly

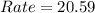`Rate = 20.59` for year 6 to 10

This means that the number of pikas increases by 20.59 yearly

So, we can say that, as year increases the number of pikas increases as opposed to when the rate reduces.