Question

Triangles GJI and PKH are similar, measurement of angle G + measure ment of angle P = 50°, and measurement of angle I is 48°. what are the measures of all the angles of these triangles?​

Answer 1

The measures of all angles in triangles GJI and PKH are as follows:

*
`\(m\angle G = m\angle P = 25°\)`

*
`\(m\angle J = m\angle K = 107°\)`

*
`\(m\angle I = m\angle H = 48°\)`

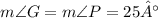
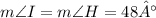
Here's how to find the measures of all the angles in triangles GJI and PKH:

1. Matching angles in similar triangles:

Since GJI and PKH are similar, their corresponding angles have the same measure.

Therefore:

* m∠G = m∠P

* m∠J = m∠K

* m∠I = m∠H (already given as 48°)

2. Using the information about angles:

* m∠G + m∠P = 50°

Substitute the first step's information:

* m∠G + m∠G = 50°

* Combine like terms:

* 2 * m∠G = 50°

* Divide both sides by 2:

* m∠G = 25°

Therefore:

* m∠P = 25° (from step 1)

3. Finding the remaining angles:

In any triangle, the sum of the angles is 180°.

* Triangle GJI:

* m∠G = 25° (found above)

* m∠I = 48° (given)

* m∠J = 180° - (m∠G + m∠I) = 180° - (25° + 48°) = 107°

* Triangle PKH:

* m∠P = 25° (found above)

* m∠H = 48° (given)

* m∠K = 180° - (m∠P + m∠H) = 180° - (25° + 48°) = 107°

Therefore:

* m∠G = m∠P = 25°

* m∠J = m∠K = 107°

* m∠I = m∠H = 48°

These are the measures of all the angles in triangles GJI and PKH.