Question

A point P os equi distant from R(-2,4) and S(6,-4) and its x co ordinate is twice its Y co ordinate find co ordinates of P

Answer 1

Answer:
`P(-4,-2)`

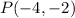
Explanation: Distance between two points is calculated as

`d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

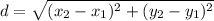
Equidistant means the same distance, i.e., the distance between points P and R is equal to the distance between points P and S.

Suppose P's y-coordinate is a. If its x-coordinate is double, then

(x,y) = (2a,a)

Thus

`\sqrt{(2a+2)^(2)+(a-4)^(2)} =\sqrt{(2a-6)^(2)+(a+4)^(2)}`

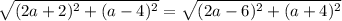
Solving

`4a^(2)+8a+4+a^(2)-8a+16=4a^(2)-24a+36+a^(2)+8a+16`

`5a^(2)+20=5a^(2)-16a+52`

`-16a=32`

`a=-2`

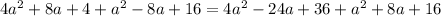
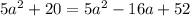
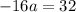
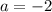
y-coordinate is
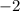`-2`, then x-ccordinate is

2a = 2(-2) =
`-4`

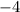
Coordinates of point P equidistant for R and S is
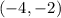`(-4,-2)`.