Question

Test the claim about the population proportion p < 0.687 given n = 225 and p = 0.662. Use α = 0.02. State your conclusion.

Answer 1

There is not enough evidence at the 0.02 significance level to support the claim that the population proportion p is less than 0.687.

To test the claim about the population proportion p<0.687 given n=225 and p=0.662 with a significance level

α=0.02, we can use a one-tailed z-test for proportions.

The formula for the z-test for proportions is:

`p= \frac{p-P}{\sqrt{(p(1-n))/(p) } }`

​Where:

p = Sample proportion

P = Claimed population proportion under the null hypothesis

n = Sample size

Given:

n=225

p=0.662

P=0.687

α=0.02

Let's calculate the z-score:

`z= \frac{0.662-0.687}{\sqrt{(0.687(0.313))/(225) } }`

`z= \frac{0.662-0.687}{\sqrt{(0.215331)/(225) } }`

`z= (0.662-0.687)/(√(0.000957) )`

`z= (-0.025)/(0.9785)`

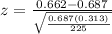
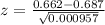
z≈−0.0256

Now, let's find the critical z-value for α=0.02. This corresponds to the left-tail test:

Using a z-table or calculator, we find that the critical z-value for

α=0.02 is approximately -2.054.

Comparing our calculated z-value (-0.0256) with the critical z-value (-2.054), since -0.0256 is greater than -2.054, we fail to reject the null hypothesis.