At
 , when
, when
 from
from
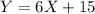 , equating with
, equating with
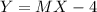 ,
,
 . The y-intercept point that satisfies both equations is
. The y-intercept point that satisfies both equations is

Given equations:
1.
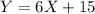
2.
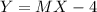
And the value
 .
.
Substitute
 into equation 1 to find the corresponding
into equation 1 to find the corresponding
 :
:
![\[Y = 6X + 15\]](https://img.qammunity.org/2024/formulas/mathematics/college/mwr3rvu1k3086t0opthlcxhangj842lehs.png)
![\[Y = 6(-2) + 15\]](https://img.qammunity.org/2024/formulas/mathematics/college/at04xl6q96cgfsjt6zas6pi1hdef8bg3lx.png)
![\[Y = -12 + 15\]](https://img.qammunity.org/2024/formulas/mathematics/college/zfoj4rx7w4gmk8szj3l5u85wbxvdjuwv8m.png)
![\[Y = 3\]](https://img.qammunity.org/2024/formulas/mathematics/college/sjvsjqq2nb641s8h9wakspdlh2xtl7atx5.png)
So, according to equation 1, when

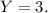
Substitute
 into equation 2 and set it equal to the previously found value of
into equation 2 and set it equal to the previously found value of
 :
:
![\[Y = MX - 4\]](https://img.qammunity.org/2024/formulas/mathematics/college/fwowgmjwqprsjziudal57ko2knla69br2n.png)
![\[3 = M(-2) - 4\]](https://img.qammunity.org/2024/formulas/mathematics/college/nmciw196jqs574t95q5u52fchi97k0utva.png)
Now, solve for
 :
:
![\[3 = -2M - 4\]](https://img.qammunity.org/2024/formulas/mathematics/college/iff6oeejzdr8galnarxxjekiaaa63w5ysg.png)
Add 4 to both sides:
3 + 4 = -2M
7 = -2M
Divide both sides by -2:
![\[M = (7)/(-2)\]](https://img.qammunity.org/2024/formulas/mathematics/college/f4nqmwgvelki55hh9ugord21vr2noelgbs.png)
![\[M = -(7)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/college/e12byd3hiwbkao2e169io7jo0vjht6tb2u.png)
Therefore, for
 to satisfy both equations, the value of
to satisfy both equations, the value of
 should be
should be
 , and the y-intercept point is
, and the y-intercept point is
 .
.