Question

What is the value of 64 ?

First, rewrite the expression as a radical raised to a power.
Enter your answer in the box.
641 = [
A
Next, evaluate the radical.
Enter your answer as the value of the radical raised to a power.
Finally, evaluate the power.
Enter your answer in the box.

Answer 1

`\large\text{$64^{(4)/(3)}=\boxed{\left(\sqrt[3]{64}\right)^4}$}`

`\large\boxed{4^4}`

`\large\boxed{256}`

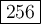
Explanation:

Given expression:

`\large\text{$64^{(4)/(3)}$}`

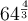
To rewrite the given expression as a radical raised to a power, we can apply the following radical rule:

`\boxed{\begin{array}{c}\underline{\sf Radical \;Rule}\\\\\large\text{$a^{(m)/(n)}=\left(\sqrt[n]{a}\right)^m$}\\\\\textsf{assuming} \;a\geq 0\end{array}}`

In this case:

• a = 64
• m = 4
• n = 3

Therefore:

`\large\text{$64^{(4)/(3)}=\left(\sqrt[3]{64}\right)^4$}`

To evaluate the radical, we can begin by rewriting 64 as 4³, then apply the radical rule:

`\boxed{\begin{array}{c}\underline{\sf Radical \;Rule}\\\\\large\text{$\sqrt[n]{a^m}=a^{(m)/(n)}$}\\\\\textsf{assuming} \;a\geq 0\end{array}}`

Therefore:

`\large\text{$\sqrt[3]{64}=\sqrt[3]{4^3}=4^{(3)/(3)}=4^1=4$}`

So:

`\large\text{$64^{(4)/(3)}=\left(\sqrt[3]{64}\right)^4=4^4$}`

In the expression 4⁴, the exponent indicates the number of times the base is multiplied by itself. So, 4⁴ is equivalent to the product of four instances of the number 4. Therefore:

`\large\text{$64^{(4)/(3)}=\left(\sqrt[3]{64}\right)^4=4^4=4 * 4 * 4 * 4=256$}`