Question

Help me answer this question

Answer 1

due to grid scaling, looking at the graph on the double-shaded area is not very obvious, but the likely suspects to be in the double-shade or namely the TRUE region are (40 , 64.50) and (30 , 80), let's check the inequalities for their TRUE / FALSE value, if both are True, then that point is in the double-shade.

`\begin{cases} 7x+12y~ \geqslant ~ 1000\\\\ x+y~ > ~ 100 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \begin{cases} x=40\\ y=64.50 \end{cases}\implies 7(40)+12(64.50)~ \geqslant ~ 1000\implies 1054~ \geqslant ~ 1000 ~~ \mathbb{TRUE} \\\\\\ \begin{cases} x=40\\ y=64.50 \end{cases}\implies 40 + 64.50~ > ~ 100\implies 104.5~ > ~ 100~~ \mathbb{TRUE} \\\\[-0.35em] ~\dotfill`

`\begin{cases} x=30\\ y=80 \end{cases}\implies 7(30)+12(80)~ \geqslant ~ 1000\implies 1170~ \geqslant ~ 1000 ~~ \mathbb{TRUE} \\\\\\ \begin{cases} x=30\\ y=80 \end{cases}\implies 30 + 80~ > ~ 100\implies 110~ > ~ 100~~ \mathbb{TRUE}`

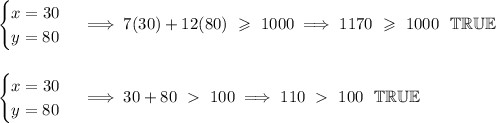
both checked out.