Question

If a fire is burning a building and it takes 2 hours to put it out using 2000 gal./min., what minimum diameter cylindrical tank 12 feet high will be needed to store the quantity needed to put out the fire?

Answer 1

The minimum diameter of the cylindrical tank needed to store the quantity needed to put out the fire is approximately 58.415 feet.

Explanation:

A gallon equals 0.134 cubic feet. First, we determine the amount of water (
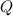`Q`), measured in cubic feet, needed to put out the fire under the assumption that water is consumed at constant rate:

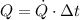`Q = \dot Q \cdot \Delta t` (1)

Where:

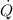`\dot Q` - Volume rate, measured in feet per minute.

`\Delta t` - Time, measured in minutes.

If we know that
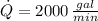`\dot Q = 2000\,(gal)/(min)` and
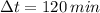`\Delta t = 120\,min`, then the amount of water is:

`Q = \left(2000\,(gal)/(min) \right)\cdot (120\,min) \cdot \left(0.134\,(ft^(3))/(gal) \right)`

`Q = 32160\,ft^(3)`

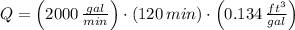
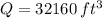
And the diameter of the cylindrical tank based on the capacity found above is determined by volume formula for a cylinder:

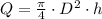`Q = (\pi)/(4)\cdot D^(2)\cdot h` (2)

Where:

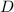`D` - Diameter, measured in feet.

`h` - Height, measured in feet.

If we know that
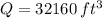`Q = 32160\,ft^(3)` and
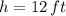`h = 12\,ft`, then the minimum diameter is:

`D^(2) = (4\cdot Q)/(\pi\cdot h)`

`D = 2\cdot \sqrt{(Q)/(\pi\cdot h) }`

`D = 2\cdot \sqrt{(32160\,ft^(3))/(\pi\cdot (12\,ft)) }`

`D \approx 58.415\,ft`

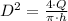
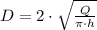
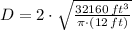
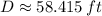
The minimum diameter of the cylindrical tank needed to store the quantity needed to put out the fire is approximately 58.415 feet.