Question

A torsion pendulum is made using a steel of radius 0.25mm and a sphere of diameter 3cm. The rigidity modulus of steel is 80GPa and density of material of a sphere is 11300kg/m^3. If the period of oscillations is 2 seconds, find the length of the wire?

Answer 1

The length of the wire is approximately 3.4593 meters

Step-by-step explanation:

The given parameters of the torsion pendulum are;

The radius of the steel holding the sphere, r = 0.25 mm = 0.00025 m

The diameter of the sphere, d = 3 cm = 0.03 m

The modulus of rigidity of steel, N = 80 GPa

The density of the material of the sphere, ρ = 11,300 kg/m³

The period of oscillation = 2 seconds

The volume of the sphere, V = 4/3 × π × R³

∴ V = 4/3 × π × (0.03/2)³ = 0.00001413716 m³

The mass of the sphere, m = V × ρ = 0.00001413716 × 11,300 ≈ 0.15975 kg

The mass of the sphere, m ≈ 0.15975 kg

The moment of inertia of a sphere, I = 2/5×m×R²

∴ I = 2/5×m×R² = 2/5 × 0.15975 kg × (0.03/2 m)² = 1.43775 × 10⁻⁵ kg·m²

The relationship between the rigidity modulus of the steel, 'N', and the length of the wire, 'l', is given as follows;

`N = (8 *\pi * I * l)/(T^2 * r^4)`

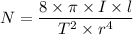
Where;

l = The length of the wire

Therefore, we have;

`l =( N * T^2 * r^4 )/(8 *\pi * I )`

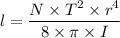
By plugging in the values, we get;

`l =( 80 * 10^9 * 2^2 * 0.00025^4 )/(8 *\pi * 1.43775 * 10^(-5) ) \approx 3.4593`

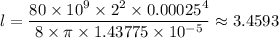
The length of the wire, l ≈ 3.4593 meters.