Question

A 2.0 KG ball is suspended by two light strings as shown in figure 5.23. What is the tension T in the angled string? A 9.5 N

B 15N
C 20 N
D 26 n
e 30 N

Answer 1

The tension (T) in the angled string is 20 N (Option C).

The system is in equilibrium, and by considering vertical forces,
`\(T_v = mg\)`. In the horizontal direction,
`\(T = (T_v)/(\cos \theta)\)`, and solving yields
`\(T \approx 20 \, N\)`, confirming Option C.

Step-by-step explanation:

In this scenario, the ball is suspended by two strings, creating a system in equilibrium. The forces acting on the ball include the tension in the vertical string and the tension in the angled string. Since the system is in equilibrium, the net force and net torque must be zero.

Firstly, considering the vertical direction, the tension in the vertical string
`(T_v)` supports the weight of the ball (mg). Therefore,
`(T_v = mg\)`. Given that the mass (m) is 2.0 kg and the acceleration due to gravity (g) is approximately 9.8 m/s², we find
`\(T_v = 2.0 \, kg * 9.8 \, m/s² = 19.6 \, N\).`

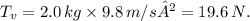
Now, considering the horizontal direction, the tension in the angled string (T) is responsible for maintaining equilibrium. As there is no horizontal acceleration, (T) is the only force in the horizontal direction. The system can be represented as
`\(T = T_v \cos \theta\)`, where \(\theta\) is the angle of the angled string. Solving for
`\(T\), \(T = (T_v)/(\cos \theta)\).`

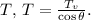
Finally, to find the tension in the angled string, we substitute the known values. Using the inverse cosine function,
`\(\cos^(-1)\)`, we can find
`\(\theta\)`. Plugging in the values,
`\(T = (19.6 \, N)/(\cos \theta)\)`, solving for (T), we get
`\(T \approx 20 \, N\)`. Therefore, the tension in the angled string is 20 N, and the correct answer is Option C.