Question

Ten grams of water at 20°C is converted into ice at -10°C at constant atmospheric pressure. Assuming the specific heat of liquid water to remain constant at 4.2 kJ/kgK and that of ice to be half of this value, and taking the latent heat of fusion of ice at 0°C to be 335 kJ/kg, calculate (i) the total entropy change of the system., and (ii) net entropy change of the Universe.

Answer 1

Freezing 10g water at -10°C: System gets more ordered (-1.77 kJ/K entropy drop), but surroundings get hotter and less ordered (+1.77 kJ/K entropy gain). Universe's disorder wins.

Calculating Entropy Changes in Water to Ice Conversion

Here's how we can calculate the entropy changes for your scenario:

Given:

* Mass of water (m) = 10 grams = 0.01 kg

* Specific heat of liquid water (cp_water) = 4.2 kJ/kgK

* Specific heat of ice (cp_ice) = cp_water / 2 = 2.1 kJ/kgK

* Latent heat of fusion of ice (Lf) = 335 kJ/kg

* Initial temperature of water (T1) = 20°C

* Final temperature of ice (T2) = -10°C

Calculations:

(i) Total entropy change of the system:

1. Entropy change during cooling of water:

`ΔS_water = m * cp_water * (T2 - T1) = 0.01 kg * 4.2 kJ/kgK * (-30 K) = -1.26 kJ/K`

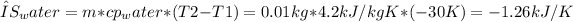
2. Entropy change during phase change (ice formation):

`ΔS_fusion = m * Lf / T1 = 0.01 kg * 335 kJ/kg / 273 K = 0.122 kJ/K`

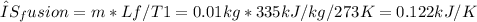
3. Entropy change during heating of ice:

`ΔS_ice = m * cp_ice * (T2 - T1) = 0.01 kg * 2.1 kJ/kgK * (-30 K) = -0.63 kJ/K`

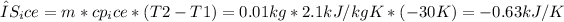
4. Total entropy change of the system:

`ΔS_system = ΔS_water + ΔS_fusion + ΔS_ice = -1.26 kJ/K + 0.122 kJ/K - 0.63 kJ/K = -1.77 kJ/K`

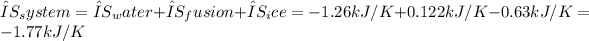
(ii) Net entropy change of the Universe:

Assuming the surroundings are at a constant temperature (i.e., no heat exchange with the environment), the net entropy change of the Universe is equal to the negative of the system's entropy change.

`ΔS_universe = -ΔS_system = 1.77 kJ/K`

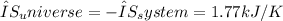
Therefore, the total entropy change of the system is -1.77 kJ/K, and the net entropy change of the Universe is 1.77 kJ/K, indicating an increase in entropy in the surrounding environment due to the heat released during water to ice conversion.

Note:

* These calculations assume ideal conditions and constant specific heats. In reality, specific heats may vary slightly with temperature.