The areas are: square (1 unit), isosceles right triangle
 units), circle
units), circle
 rectangle (1 unit), and equilateral triangle
rectangle (1 unit), and equilateral triangle
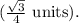
Let's denote the side length of the square as \(s\). Since the area of the square is 1 square unit, we have:
![\[s^2 = 1\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/oit16yl8nlqqy19znfsgbshhz1cg4krm2m.png)
So,
 (since the side length cannot be negative).
(since the side length cannot be negative).
Now, for one triangle, let's consider an isosceles right triangle with legs of length
 The area of a triangle is given by the formula:
The area of a triangle is given by the formula:
![\[A_{\text{triangle}} = (1)/(2) * \text{base} * \text{height}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rjdysbcmeexw32kgq3tydo8k0qnw2va5hi.png)
In this case, the base and height are both \(s/2\), so:
![\[A_{\text{triangle}} = (1)/(2) * (s)/(2) * (s)/(2) = (s^2)/(8) = (1)/(8)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3phoi2sf6heve6lcx57h5xckqo8rt3sm9u.png)
So, the area of one triangle is
 square units.
square units.
Now, let's consider other shapes:
1. Circle:
The area of a circle is given by the formula
 where \(r\) is the radius. Since the square's side length is \(s = 1\), the radius of the circle that can fit inside the square is
where \(r\) is the radius. Since the square's side length is \(s = 1\), the radius of the circle that can fit inside the square is
 Therefore:
Therefore:
![\[A_{\text{circle}} = \pi * \left((1)/(2)\right)^2 = (\pi)/(4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1t6s2hbusq5cjtzociwrgqtvz0piykhots.png)
2. Rectangle:
Let's consider a rectangle with dimensions
 . The area of the rectangle is given by
. The area of the rectangle is given by
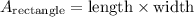
![\[A_{\text{rectangle}} = 2s * (s)/(2) = s^2 = 1\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/t34ynz15955qs83d46lw8qfbm13d8v8gx9.png)
3. Equilateral Triangle:
The area of an equilateral triangle with side length \(s\) is given by
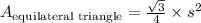
![\[A_{\text{equilateral triangle}} = (√(3))/(4) * 1^2 = (√(3))/(4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lk5a7y4vqpoucpg3hfg4b1f7nbnj49r5cl.png)
These are a few examples of shapes with different areas that can be related to the original square and triangle.