Question

F(x)=8x/x^2-4 determine the symmetry, what is the y-intercept what is the x-intercept, find the vertical asymptotes find the horizontal asymptote

Answer 1

The vertical asymptotes occur at x=2 and x=−2 since these values make the denominator zero.

The horizontal asymptote is y=0.

Let's break down each part of this function step by step.

The given function is

`f(x)= (8x)/(x^2-4)`

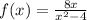
Symmetry:

To determine symmetry, let's analyze the function.

`f(x)= (8(-x))/((-x)^2-4) =(-8x)/(x^2-4)`

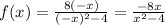
Comparing f(x)=f(−x), we see that f(x) is not equal to f(−x), which means the function is not even. Let's check for odd symmetry:

f(−x)=−f(x)

`(-8x)/((-x)-4) = -(8x)/((-x)-4)`

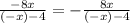
Since the equation holds true, the function is odd symmetric about the origin.

Y-intercept:

The y-intercept is found by setting

f(0)=
`(8(0))/(0^2-4) =(0)/(-4) =0`

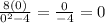
So, the y-intercept is at the point (0, 0).

X-intercept:

To find the x-intercept, set y=0 and solve for x:

`0 =(8x)/(x^2-4)`

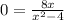
​This implies 8x=0 which gives x=0.

However, the denominator cannot be zero, so let's find the values of x that make the denominator zero:

x^2 −4=0

x^2 =4

x=±2

Therefore, the x-intercepts are at the points (-2, 0) and (2, 0).

Vertical Asymptotes:

Vertical asymptotes occur when the denominator becomes zero and the numerator doesn't.

In this case, the vertical asymptotes occur at x=2 and x=−2 since these values make the denominator zero.

Horizontal Asymptote:

To find the horizontal asymptote, examine the behavior of the function as

x approaches positive or negative infinity.

lim x→∞
`(8x)/(x^2-4) =0`

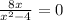
lim x→−∞
`(8x)/(x^2-4) =0`

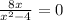
Both the limits as x approaches infinity and negative infinity are zero. Therefore, the horizontal asymptote is y=0.