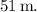The magnitude (distance) of the vector is approximately
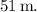
To find the magnitude (distance) of the vector given its components in the x and y directions
 and
and
 , you can use the Pythagorean theorem. The magnitude
, you can use the Pythagorean theorem. The magnitude
 is given by:
is given by:
![\[ A = √(A_x^2 + A_y^2) \]](https://img.qammunity.org/2024/formulas/physics/college/uqwbgi9hqwrkdsaui5kr87e9l78j50yll4.png)
Given your values:
![\[ A_x = 44.4 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/college/v944um3lm3petu21lmp1jyxawluu5m4p3z.png)
![\[ A_y = 25.1 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/college/mufgzeniflkcrr8b1wf5khx2249i9oj7s5.png)
Substitute these values into the formula:
![\[ A = \sqrt{(44.4 \, \text{m})^2 + (25.1 \, \text{m})^2} \]](https://img.qammunity.org/2024/formulas/physics/college/acsjasiik902xee6lh80rh5sa6qortwjqq.png)
![\[ A = √(1971.36 + 630.01) \]](https://img.qammunity.org/2024/formulas/physics/college/37po8zbwywlur5npzxsdjbrz9pe0yw36ze.png)
![\[ A = √(2601.37) \]](https://img.qammunity.org/2024/formulas/physics/college/ursitb7w0unh7ndv1xyup20cg4k7o0vagh.png)
![\[ A \approx 51 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/college/sdm4720ya4r80dc086ny0i4czjxomvx3sg.png)
Therefore, the magnitude (distance) of the vector is approximately