Using a graphing utility, plot
 and
and
 in the interval
in the interval
 to visualize the curve's behavior.
to visualize the curve's behavior.
To graph the curve represented by the parametric equations
 and
and
 in the given interval
in the given interval
 ., we can use a graphing utility.
., we can use a graphing utility.
1. Set up the graphing utility to plot parametric equations.
2. Enter the parametric equations:
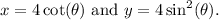
3. Define the parameter range as

4. Generate the graph.
The resulting curve will exhibit the shape defined by the parametric equations within the specified interval. The cotangent function will influence the behavior of x, while the squared sine function will impact y. Analyzing the graph will provide insights into the curve's characteristics and how it evolves as the parameter
 changes.
changes.