The circumference of the base changing when the radius is 8 inches is
 . The area of the base changing at rate
. The area of the base changing at rate
 when the radius is 8 inches. The volume of the sand cone is changing at rate of
when the radius is 8 inches. The volume of the sand cone is changing at rate of
 . The string of the kite is being let out at a rate of 3 ft/sec
. The string of the kite is being let out at a rate of 3 ft/sec
For problem 11:
Given:
The radius of the base (r) is twice its height (h), i.e., r = 2h.
- The radius of the base is increasing at the rate of 6 inches per minute,
 inches/min.
inches/min.
a) What rate is the circumference of the base changing when the radius is 8 inches?
The circumference of the base (C) of the cone is given by
 . We are asked to find
. We are asked to find
 when r = 8.
when r = 8.
![\[ C = 2\pi r \]](https://img.qammunity.org/2024/formulas/mathematics/college/2g81x2jgcscb7dbl8hkpqxri760v3y89ad.png)
![\[ (dC)/(dt) = 2\pi (dr)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/college/mcw7x82fukvg5jl1wp6756hf1zv0fbep4l.png)
Substitute the given values:
![\[ (dC)/(dt) = 2\pi \cdot 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/gu6et4aw5uq5e6me46beo607tc2w34qpr5.png)
![\[ (dC)/(dt) = 12\pi \text{ inches/min} \]](https://img.qammunity.org/2024/formulas/mathematics/college/wx8cql92y5ls5jt2nhff05tbk92wowd5ku.png)
b) What rate is the area of the base changing when the radius is 8 inches?
The area of the base (A) of the cone is given by
 . We are asked to find
. We are asked to find
 when r = 8.
when r = 8.
![\[ A = \pi r^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qwbt4bafc09o8qjpxjdy22m5nos713v5hl.png)
![\[ (dA)/(dt) = 2\pi r (dr)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/college/chxmet3xgnca8vxbrc3vkftno2uz9mb9k0.png)
Substitute the given values:
![\[ (dA)/(dt) = 2\pi \cdot 8 \cdot 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/o604qodpseesnxmh546icaqf0syx4ko6k4.png)
![\[ (dA)/(dt) = 96\pi \text{ square inches/min} \]](https://img.qammunity.org/2024/formulas/mathematics/college/n647twfndzdj7ic8nnf04dnmuzslvk752d.png)
c) What rate is the volume of the sand cone changing when its height is 5 feet?
The volume (V) of the cone is given by
 . We are asked to find
. We are asked to find
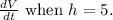
![\[ V = (1)/(3)\pi r^2h \]](https://img.qammunity.org/2024/formulas/mathematics/college/btnt28ta6fq1zh7p8xcbihwzc500foi4ys.png)
![\[ (dV)/(dt) = (1)/(3)\pi (2h) (dr)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/college/96hykg7shxzx8nk4oga91rqx6a435av3s8.png)
Substitute the given values:
![\[ (dV)/(dt) = (1)/(3)\pi (2 \cdot 5) \cdot 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/jmvk12e66mgqxhhrg14h0m0gongz1lz6xy.png)
![\[ (dV)/(dt) = 20\pi \text{ cubic feet/min} \]](https://img.qammunity.org/2024/formulas/mathematics/college/fp56jiht6ov3jmpgbatyfjv0zoyw62qzdn.png)
For problem 12:
Given:
- Height of the kite (h) is 40 ft.
- The string is being let out horizontally at a rate of 3 ft/sec,
 ft/sec.
ft/sec.
- The length of the string (s) released is 50 ft.
We want to find
 when s = 50.
when s = 50.
Using the Pythagorean theorem for right triangles
 , we can differentiate both sides with respect to time (t):
, we can differentiate both sides with respect to time (t):
![\[ 2s (ds)/(dt) = 2h (dh)/(dt) + 2x (dx)/(dt) \]](https://img.qammunity.org/2024/formulas/mathematics/college/6g57jz09p15m18ejgj3lt0revk0pi3dyci.png)
Now, substitute the given values and solve for
 :
:
![\[ 2 \cdot 50 \cdot (ds)/(dt) = 2 \cdot 40 \cdot 0 + 2 \cdot 3 \cdot 50 \]](https://img.qammunity.org/2024/formulas/mathematics/college/rq98rbvxspu3fqg8vb5zim4ta9fy8v0sia.png)
![\[ 100 (ds)/(dt) = 300 \]](https://img.qammunity.org/2024/formulas/mathematics/college/czbbgojk01wrpx13qhtr0hyym8vrrbpb30.png)
![\[ (ds)/(dt) = 3 \text{ ft/sec} \]](https://img.qammunity.org/2024/formulas/mathematics/college/64g49j0wua3xn06lwyo57roype63b753gm.png)
So, at the given moment, the string is being let out at a rate of 3 ft/sec.