Question

Find all zeros real and/or imaginary, for the function f(x)=4x^3-3x^2 20x-15

Answer 1

The zeros of the cubic function
`f(x)=4x^(3)-3x^(2)-20x-15` are x=3 (real) and two complex conjugate roots
`x=(-9+i√(-71 ) )/(8)`,
`x=(-9-i√(-71 ) )/(8)`.

The given cubic function is
`f(x)=4x^(3)-3x^(2)-20x-15` and we want to find its zeros.

Start by setting the function equal to zero:

`f(x)=4x^(3)-3x^(2)-20x-15=0`

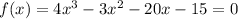
Now, try to find a rational root using the Rational Root Theorem. The possible rational roots are factors of the constant term (15) divided by factors of the leading coefficient (4). The potential rational roots are ±1, ±3, ±5, ±15.

Upon testing, we find that x=3 is a root. Using synthetic division or polynomial long division, we can factor the cubic equation:

`4x^(3)-3x^(2)-20x-15=(x-3)(4x^(2) +9x+5)`

Now, focus on the quadratic factor
`(4x^(2) +9x+5)`

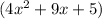
Solve this quadratic equation using the quadratic formula:

`x=\frac{-b+/-\sqrt{b^(2)-4ac } }{2a}`

For
`4x^(2) +9x+5` a=4, b=9, and c=5. Plugging in these values:

`x=\frac{-9+/-\sqrt{9^(2)-4(4)(5) } }{2(4)}`

Simplifying the expression under the square root gives an imaginary result:

`x=(-9+/-√(-71 ) )/(8)`

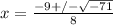
Therefore, the real zero is x=3, and the complex zeros are given by:

`x=(-9+i√(-71 ) )/(8)` ,
`x=(-9-i√(-71 ) )/(8)`

In summary, the zeros of the cubic function
`f(x)=4x^(3)-3x^(2)-20x-15` are x=3 (real) and two complex conjugate roots.

​

​

​