This computation provides an approximate doubling time of 25.46 years when using the change-of-base formula for logarithms.
The formula given is 2=1+ r/n^{nt}), where:
r is the annual interest rate (in decimal form),
n is the number of times the interest is compounded per year, and
t is the time in years.
For an investment at 11% compounded quarterly (n=4), we have:
2= 1 + (0.11/4)^4t
First, solve for t using logarithmic form to solve for the exponent:
2= (1+ 0.11/4)^4t
2=(1.0275)^4t
Taking the natural logarithm of both sides:
ln(2)=ln(1.0275)^4t
ln(2)=4t⋅ln(1.0275)
Now, solve for t:
t= ln(2)/ 4⋅ln(1.0275)
Using a calculator to compute this:
t≈ ln(2)/ 4⋅ln(1.0275)
≈ 0.6931/ 4⋅0.0272
≈6.42
So, the doubling time for an investment at 11% compounded quarterly is approximately 6.42 years.
If you're required to use a change-of-base formula (logarithmic form), the change-of-base formula for logarithms is:
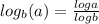
You could use this formula to find the doubling time:
t= log(2)/ log(1.0275)
t≈ 0.6931/ 0.0272
≈25.46
This computation provides an approximate doubling time of 25.46 years when using the change-of-base formula for logarithms.
Question
Use the formula 2 = 1 + r 100n nt to find the doubling time t, in years, for an investment at r % compounded n times per year. Write this exponential statement in logarithmic form for an investment at 11% compounded quarterly. t = Use a change-of-base formula to find the doubling time (in years) for this investment. (Round your answer to two decimal places.) t = Incorrect: Your answer is incorrect.