The reactions at supports A and B are:
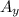 = F * (L - a) / L and
= F * (L - a) / L and
 = F * a / L. The laws for the internal statics quantities of the beam are: Transfer force = Shear force; Attack moment = Bending moment and Axial force = Normal force
= F * a / L. The laws for the internal statics quantities of the beam are: Transfer force = Shear force; Attack moment = Bending moment and Axial force = Normal force
Determining Reactions at Supports:
To determine the reactions at supports, we can use two equilibrium equations:
∑
 = 0
= 0
∑
 = 0
= 0
where:
∑
 is the sum of all forces in the y-direction
is the sum of all forces in the y-direction
∑
 is the sum of all moments about point A
is the sum of all moments about point A
Since the beam is in static equilibrium, the sum of all forces and moments must be equal to zero.
Determining Reaction at A
To determine the reaction at A, we can take the sum of moments about point B. This gives us:
∑
 = 0
= 0
F(L - a) -
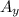 * L = 0
* L = 0
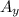 = F * (L - a) / L
= F * (L - a) / L
Determining Reaction at B
To determine the reaction at B, we can take the sum of forces in the y-direction. This gives us:
∑
 = 0
= 0
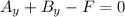
 = F -
= F -
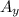
 = F * a / L
= F * a / L
Laws for Internal Statics Quantities
The three internal statics quantities of a beam are:
Transfer force - The force that is transferred from the beam to the support.
Attack moment - The moment that is applied to the beam by the support.
Axial force - The force that acts along the axis of the beam.
The laws for the internal statics quantities of a beam can be summarized as follows:
Transfer force - The transfer force at a point is equal to the shear force at that point.
Attack moment - The attack moment at a point is equal to the bending moment at that point.
Axial force - The axial force at a point is equal to the normal force at that point.