Question

A student is graduating from college in six months but will need a loan in the amount of $3,725 for the last semester. The student may receive either an unsubsidized Stafford Loan or a PLUS Loan. The terms of each loan are: Unsubsidized Stafford Loan: annual interest rate of 4.65%, compounded monthly, with a balance of $3,901.95, at the time of repayment PLUS loan: annual interest rate of 5.65%, compounded monthly with payment deferred until graduation Which loan will have a lower balance and by how much at the time of repayment? The Stafford Loan will have a lower balance by $70.47 at the time of repayment. The PLUS Loan will have a lower balance by $70.47 at the time of repayment. The Stafford Loan will have a lower balance by $16.72 at the time of repayment. The PLUS Loan will have a lower balance by $16.72 at the time of repayment.

Answer 1

The Loan will have a lower balance by 70.47 at the time of repayment.

How to Identify the best loan offer?

To determine which loan will have a lower balance at the time of repayment, we need to calculate the total amount of interest that will be accrued on each loan.

1) For the unsubsidized Stafford loan:

The loan amount is $3,725.

The annual interest rate is 4.65%, compounded monthly. This means the monthly interest rate is 4.65%/12 = 0.3875%.

The loan will be repaid in 6 months, so there will be 6 monthly compounding periods.

Using the formula for compound interest, the balance of the loan at the time of repayment will be:

balance = principal x (1 + monthly interest rate)^number of compounding periods

balance =
`$3,725 x (1 + 0.003875)^6`

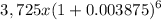
balance = 3,901.95

So the balance of the unsubsidized Stafford loan at the time of repayment will be 3,901.95.

2) For the PLUS loan:

The loan amount is 3,725.

The annual interest rate is 5.65%, compounded monthly. This means the monthly interest rate is 5.65%/12 = 0.4708%.

The loan will be deferred until graduation, which is in 6 months, so there will be 6 monthly compounding periods.

Using the formula for compound interest, the balance of the loan at the time of repayment will be:

balance = principal x (1 + monthly interest rate)^number of compounding periods

balance =
`$3,725 * (1 + 0.004708)^6`

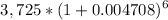
balance = 3831.47

So the balance of the PLUS loan at the time of repayment will be 3831.47

Difference in balance = 3,901.95 - 3831.47

= 70.47

Therefore, the PLUS loan will have a lower balance at the time of repayment, by an amount of 70.47