Answer:
4 meters
Step-by-step explanation:
To find the distance traveled by the marble before stopping, we can use the kinematic equation that relates initial velocity (
 ), acceleration (
), acceleration (
 ), and displacement (
), and displacement (
 ):
):

Where:
-
 is the final velocity (which is 0 when the marble stops),
is the final velocity (which is 0 when the marble stops),
-
 is the initial velocity,
is the initial velocity,
-
 is the acceleration, and
is the acceleration, and
-
 is the displacement.
is the displacement.
In this case,
Substitute these values into the equation:
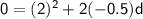
Simplify and solve for
 :
:
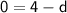
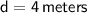
So, the marble travels
 before stopping.
before stopping.