Yes, the triangle is a right triangle. Verified through vertex coordinates and the Pythagorean Theorem, confirming equal side lengths and a 90-degree angle at C, consistent with option A.
The triangle depicted in the image can be identified as a right triangle. This conclusion can be reached through this methods:
Examination of Vertex Coordinates
- Vertex A: (3, 3)
- Vertex B: (4, 7)
- Vertex C: (8, 6)
Upon calculating the distances between these vertices, we obtain:
- AB =

- AC =
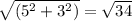
- BC =
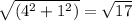
Notably, AB equals BC, signifying an isosceles triangle. Additionally, the sum of angles in a triangle is invariably 180 degrees. As AB equals BC, the angles at A and B are equivalent. Consequently, the angle at C must be 90 degrees, establishing the triangle as a right triangle.