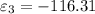The induced e.m.f at the right angle to the plane of the field is zero. The induced e.m.f in the plane of the field is -142.45 and The induced e.m.f at 45 with the field direction is -116.31
To calculate the instantaneous value of the induced electromotive force (e.m.f.) in each of the given orientations of the coil, we can use Faraday's law of electromagnetic induction, which states that the induced e.m.f.
 is equal to the negative rate of change of magnetic flux through the coil.
is equal to the negative rate of change of magnetic flux through the coil.
The formula for the induced e.m.f.
 is given by:
is given by:
![\[ \varepsilon = -N (d\Phi)/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/aw5n335hjsw6wg4rtncxd4ls6kw3wcqh6t.png)
Where:
-
 is the induced e.m.f.
is the induced e.m.f.
-
 is the number of turns in the coil.
is the number of turns in the coil.
-
 is the rate of change of magnetic flux.
is the rate of change of magnetic flux.
The magnetic flux
 through a coil is given by the product of the magnetic field
through a coil is given by the product of the magnetic field
 , the area
, the area
 of the coil, and the cosine of the angle
of the coil, and the cosine of the angle
 between the normal to the coil and the magnetic field:
between the normal to the coil and the magnetic field:
![\[ \Phi = B \cdot A \cdot \cos(\theta) \]](https://img.qammunity.org/2024/formulas/engineering/college/7amdjtt5gsutcxlngepwkumu2g18tc2j00.png)
Now, let's calculate the instantaneous values of the induced e.m.f. for the three given orientations:
(i) At right angles to the plane of the field
 :
:
![\[ \varepsilon_1 = -N (d(B \cdot A \cdot \cos(90^\circ)))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/ououhrs2zqcduo8xvbtn5vu371b5rg4zh8.png)
(ii) In the plane of the field
 :
:
![\[ \varepsilon_2 = -N (d(B \cdot A \cdot \cos(0^\circ)))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/6alfmob6no9h4v2o9swlzuopber4lqrojt.png)
(iii) At 45 degrees with the field direction
 :
:
![\[ \varepsilon_3 = -N (d(B \cdot A \cdot \cos(45^\circ)))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/sgwqoobe70qg81gwmktokhuzf7h1ycwcio.png)
Given values:
- Side length of the square coil
 = 10 cm = 0.1 m
= 10 cm = 0.1 m
- Number of turns
 = 100
= 100
- Magnetic field strength
 = 0.5 Wb/m²
= 0.5 Wb/m²
- Angular speed
 =
=
 radians/second
radians/second
The area
 of the coil is
of the coil is
 .
.
Now, calculate the instantaneous values for each orientation.
(i) At right angles to the plane of the field
 :
:
![\[ \varepsilon_1 = -N (d(B \cdot A \cdot \cos(90^\circ)))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/ououhrs2zqcduo8xvbtn5vu371b5rg4zh8.png)
Since
 , the induced e.m.f.
, the induced e.m.f.
 for this orientation is zero.
for this orientation is zero.
(ii) In the plane of the field
 :
:
![\[ \varepsilon_2 = -N (d(B \cdot A \cdot \cos(0^\circ)))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/6alfmob6no9h4v2o9swlzuopber4lqrojt.png)
Since
 , the induced e.m.f.
, the induced e.m.f.
 for this orientation is given by:
for this orientation is given by:
![\[ \varepsilon_2 = -N (d(B \cdot A))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/b4s3zz9o9uqx6b680k65xjyygxnuekj4kz.png)
Substitute the values:
![\[ \varepsilon_2 = -100 (d(0.5 \cdot 0.1^2))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/8xuctfty7mp9uceqoj8gznvrhgwmrr9rxl.png)
(iii) At 45 degrees with the field direction
 :
:
![\[ \varepsilon_3 = -N (d(B \cdot A \cdot \cos(45^\circ)))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/sgwqoobe70qg81gwmktokhuzf7h1ycwcio.png)
Since
 =
=
 , the induced e.m.f.
, the induced e.m.f.
 for this orientation is given by:
for this orientation is given by:
![\[ \varepsilon_3 = -100 (d(0.5 \cdot 0.1^2 \cdot (√(2))/(2)))/(dt) \]](https://img.qammunity.org/2024/formulas/engineering/college/7ubn8gew60vldkgdr64vco3j4grb7g0vq5.png)
Now, differentiate the expressions for
 and
and
 with respect to time and substitute the values to get the final calculations. Note that
with respect to time and substitute the values to get the final calculations. Note that
 is the angular speed.
is the angular speed.
![\[ \varepsilon_2 = -100 \cdot 2 \pi \omega \cdot 0.5 \cdot 0.1^2 \]](https://img.qammunity.org/2024/formulas/engineering/college/finh39g9ztagfkwkbt378lxnr8768qnt5d.png)
![\[ \varepsilon_3 = -100 \cdot 2 \pi \omega \cdot 0.5 \cdot 0.1^2 \cdot (√(2))/(2) \]](https://img.qammunity.org/2024/formulas/engineering/college/u5od7z2eerariyrls62kot5lblu48iy5u9.png)
Now, substituting the given values for
 we get:
we get:
![\[ \varepsilon_2 = -100 \cdot 2 \pi \left((500 \pi)/(30)\right) \cdot 0.5 \cdot 0.1^2 \]](https://img.qammunity.org/2024/formulas/engineering/college/qc4zunmgpiqcm3drfsdly0repit6s685px.png)
![\[ \varepsilon_3 = -100 \cdot 2 \pi \left((500 \pi)/(30)\right) \cdot 0.5 \cdot 0.1^2 \cdot (√(2))/(2) \]](https://img.qammunity.org/2024/formulas/engineering/college/wodziqr4zlszl863ls5hspd0l2sn0zfjk4.png)
![\[ \varepsilon_2 =-142.45 \]](https://img.qammunity.org/2024/formulas/engineering/college/61uc2mi4ky6ebmyskj2zma46j77z1nmjpi.png)