The end behavior of the polynomial functions is determined by their leading terms, with
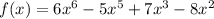
 rising to the right, and f(x) = 4x(x - 4)(x + 2) falling to the left and rising to the right.
rising to the right, and f(x) = 4x(x - 4)(x + 2) falling to the left and rising to the right.
The end behavior of a polynomial function is determined by the leading term, which is the term with the highest exponent. Let's analyze each polynomial function:
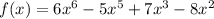 The leading term is
The leading term is
 . Since, the coefficient is positive and the exponent is even, the end behavior is 3. Rises to the left and rises to the right.
. Since, the coefficient is positive and the exponent is even, the end behavior is 3. Rises to the left and rises to the right.
 The leading term is
The leading term is
 . Since the coefficient is negative and the exponent is odd, the end behavior is 2. Rises to the left and falls to the right.
. Since the coefficient is negative and the exponent is odd, the end behavior is 2. Rises to the left and falls to the right.
f(x) = 4x(x - 4)(x + 2): The leading term when expanded is
 . Since the coefficient is positive and the exponent is odd, the end behavior is 1. Falls to the left and rises to the right.
. Since the coefficient is positive and the exponent is odd, the end behavior is 1. Falls to the left and rises to the right.