Final Answer:
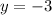
Taking the cube root of both sides in the equation
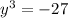 , we find that
, we find that
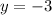 is the solution. This is because
is the solution. This is because
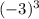 equals -27, satisfying the given cubic equation.
equals -27, satisfying the given cubic equation.
Step-by-step explanation:
The given equation is
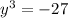 . To find the solution, we can use the fact that the cube root of -27 is -3. Therefore,
. To find the solution, we can use the fact that the cube root of -27 is -3. Therefore,
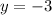 is the solution to the equation.
is the solution to the equation.
In detail, to solve for \(y\), we take the cube root of both sides of the equation. The cube root of -27 is -3, a
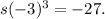 So,
So,
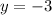 is the solution that satisfies the equation. It's important to note that in cubic equations, there may be only one real solution or multiple solutions, including complex roots. However, in this case, the solution is a real number, -3.
is the solution that satisfies the equation. It's important to note that in cubic equations, there may be only one real solution or multiple solutions, including complex roots. However, in this case, the solution is a real number, -3.
In mathematical terms, the cube root function denoted as \(\sqrt[3]{x}\) is the inverse of raising a number to the power of 3. In this particular equation,
![\(\sqrt[3]{-27} = -3\),](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/ndd1stn3k8txqmeqxo10.png) and thus,
and thus,
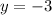 is the solution that satisfies the given cubic equation. This process demonstrates how the understanding of basic arithmetic operations and inverse functions can be applied to solve equations involving cube roots.
is the solution that satisfies the given cubic equation. This process demonstrates how the understanding of basic arithmetic operations and inverse functions can be applied to solve equations involving cube roots.