The enclosure formed by the vertices A(-4,-3), B(3,-4), C(8,1), and D(1,2) is a quadrilateral in the coordinate plane. To gain insights into its properties, we can examine its sides, angles, and other geometric characteristics.
Firstly, we can calculate the lengths of the sides using the distance formula. For instance, the length of AB is given by the distance formula as follows:
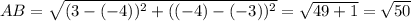
Similarly, the lengths of BC, CD, and DA can be determined. This information helps us identify the type of quadrilateral. If all sides are equal, it is a rhombus; if opposite sides are equal, it is a parallelogram, and so on.
The slope of each side can be found using the coordinates of the vertices. This enables us to analyze the angles formed by these sides. For example, the slope of AB is
. The angle formed by AB and BC can be determined by finding the arctangent of the difference in slopes.
The enclosure's area can be calculated using the shoelace formula, which requires ordering the vertices in either a clockwise or counterclockwise direction.
In summary, by employing distance formulas, slope calculations, and geometric formulas, we can thoroughly understand the properties of the enclosure, enabling us to classify it and determine various geometric features.
Complete question
An enclosure shaped like a quadrilateral ABCD is erected in a park. Assuming that the park is a coordinate plane, the posts of the enclosure can be represented by vertices A(-4,-3), B(3,-4), C(8,1) , and D(1,2)