
Answer :
Note: To solve a problem like this, we must first determine which of the two numbers add 5 and multiply 6, we know that they are 2 and 3 and then we must Rewrite the expression using the above.
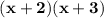
Now, we must put a fraction since we can more easily solve the problem posed.
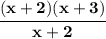
Now the last thing we have to do is Cancel
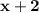 to have a final result that is the following:
to have a final result that is the following:
