Question

To understand the relationships of the energetics, forces, acceleration, and velocity of an oscillating pendulum, and to determine how the motion of a pendulum depends on the mass, the length of the string, and the acceleration due to gravity.

For this tutorial, use the PhET simulation Pendulum Lab. This simulation mimics a real pendulum and allows you to adjust the initial position, the mass, and the length of the pendulum.
You can drag the pendulum to an arbitrary initial angle and release it from rest. You can adjust the length and the mass of the pendulum using the slider bars at the top of the green panel. Velocity and acceleration vectors can be selected to be shown, as well as the forms of energy.


I. Now, keep the mass fixed to any value you choose and measure the period for several different pendulum lengths. How does the period of the pendulum depend on the length?

Answer 1

The period of a pendulum is directly proportional to the square root of its length, according to the relationship:
`\(T \propto √(L)\)`, where T is the period and L is the length of the pendulum. Therefore, as the length of the pendulum increases, the period also increases.

Step-by-step explanation:

In classical mechanics, the period of a simple pendulum—the time it takes to complete one full oscillation—is influenced by various factors. One fundamental relationship is expressed by the formula
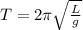`\(T = 2\pi \sqrt{(L)/(g)}\)`, where T is the period, L s the length of the pendulum, and g is the acceleration due to gravity. To isolate the dependence on length, we can rearrange the equation to
`\(T \propto √(L)\)`, emphasizing that the period is directly proportional to the square root of the length.

This relationship arises from the balance between gravitational potential energy and kinetic energy as the pendulum swings. As the length increases, the potential energy increases, resulting in a longer period. This dependence on the square root of length aligns with the theoretical expectations for simple harmonic motion.

Conducting experiments with the PhET Pendulum Lab, fixing the mass and altering the length while measuring the period, reaffirms this relationship. Observing the changing periods for different lengths allows for a practical confirmation of the theoretical expectations.

The simulations enable a hands-on exploration of the physics behind pendulum motion and provide a valuable tool for understanding the interplay of variables in simple harmonic oscillators.