To determine the duration and the maximum height of a bottle rocket's flight, as well as its path equation, one applies the equations of projectile motion, considering the acceleration due to gravity and the initial launch velocity provided.
When analyzing the motion of a bottle rocket launched vertically, we can apply the principles of projectile motion. The initial upward velocity and the distance it landed from the launch site are key information given for solving parts (a) and (b). For part (c), we need to write an equation modeling rocket's trajectory.
For part (a): The total time a projectile is in the air can be found by using the equation:
- Time = (2 * Initial Velocity) / Acceleration due to gravity (g)
However, we have to adjust the units since g should be in feet per second squared (ft/
) which is approximately 32 ft/
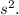
For part (b): Maximum height attained by the rocket can be calculated by using the formula:
- Max Height =
/ (2 * g)
Again, we have to ensure that g is in the correct units.
For part (c): The equation that models the path of the bottle rocket with respect to distance and height takes the form of:
- y = -0.5 * g * t2 + Initial Velocity * t
By substituting the given initial velocity and the value of g, one can find the equation specific to this case, where 'y' is the height and 't' is the time after launch.
For the sketch, it's important to label all principal parts including the launch point, the maximum height reached, and the landing point 50 feet away from launch.