Question

FIlowing question is about the r(x)=((x+1)(x-2))/((x+2)(x-6)) unction r has horizontal asymp

Answer 1

The function
`\( r(x) = \frac{{(x+1)(x-2)}}{{(x+2)(x-6)}} \)` has horizontal asymptotes at
`\( y = (1)/(1) \) and \( y = (-1)/(1) \).`

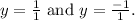
Step-by-step explanation:

To identify the horizontal asymptotes of the function
`\( r(x) \),` we examine the behavior of the function as
`\( x \)` approaches positive and negative infinity. For the given function,
`\( r(x) = \frac{{(x+1)(x-2)}}{{(x+2)(x-6)}} \)` , the degrees of the numerator and denominator are the same (both are quadratic), so we compare the leading coefficients.

The horizontal asymptotes are determined by the ratio of the leading coefficients, which are 1 in both cases. Therefore, the horizontal asymptotes are
`\( y = (1)/(1) \) and \( y = (-1)/(1) \).`

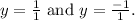
As
`\( x \)` approaches positive or negative infinity, the terms with the highest power dominate the function. In this case, the horizontal asymptotes
`\( y = 1 \) and \( y = -1 \)` represent the values that
`\( r(x) \) approaches as \( x \)` becomes infinitely large or infinitely small.

The function does not cross or touch these asymptotes; rather, it gets arbitrarily close to them as
`\( x \)` moves towards infinity or negative infinity. The identified horizontal asymptotes provide insights into the long-term behavior of the function.