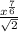Question

Radical form of (x^2/3 • X ^5/3)^1/2

Answer 1

The radical form of the expression
`(\frac{x^{(2)/(3) }. x^{(5)/(3) }}{2} )^{(1)/(2) }` is
`\frac{x^{(7)/(6) }}{√(2) }`.

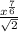To find the radical form of
`(\frac{x^{(2)/(3) }. x^{(5)/(3) }}{2} )^{(1)/(2) }` , let's simplify it step by step.

First, let's combine the exponents inside the parentheses:

`x^{(2)/(3) }. x^{(5)/(3) }= x^{(2)/(3) +(5)/(3) }= x^{(7)/(3) }`

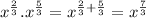
So, the expression becomes:

`(\frac{x^{(7)/(3) }}{2} )^{(1)/(2) }`

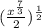
To simplify further, recall that raising something to the power of 1/2 is the same as taking the square root:

`\sqrt{\frac{x^{(7)/(3) }}{2}}`

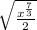
In radical form:

`\sqrt{\frac{x^{(7)/(3) }}{2}}=\sqrt{\frac{x^{(7)/(3) }}{√(2) } } =\frac{x^{(7)/(3) }}{√(2) }`

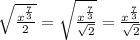
Therefore, the radical form of the expression
`(\frac{x^{(2)/(3) }. x^{(5)/(3) }}{2} )^{(1)/(2) }` is
`\frac{x^{(7)/(6) }}{√(2) }`