Question

Determine whether s(t)=0.65(0.48)^t represents exponential growth or exponential decay. The function represents exponential decay .The percent rate of change is %

Answer 1

The function
`\( s(t) = 0.65(0.48)^t \)` represents exponential decay. The decay factor is
`\(0.48\)` indicating a percent rate of change of
`\(-52\%\),`signifying a decrease over time.

The given function
`\( s(t) = 0.65 * (0.48)^t \)`represents exponential decay. In general, an exponential function of the form
`\( s(t) = a * b^t \)`represents exponential growth if
`\( 0 < b < 1 \)` and exponential decay if
`\( b > 1 \).`

In this case, the base of the exponential term is
`\( 0.48 \),` which is between
`\( 0 \) and \( 1 \)`. Therefore, the function represents exponential decay.

To find the percent rate of change, you can use the formula for exponential decay:

`\[ s(t) = a * b^t \]`

where:

-
`\( a \)` is the initial quantity,

-
`\( b \)` is the decay factor (in this case,
`\( 0.48 \)),`

-
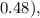
`\( t \)` is time.

In your function, \( a = 0.65 \) and \( b = 0.48 \). The percent rate of change is given by \( r = (b - 1) \times 100\% \). Substituting the values, you get:

`\[ r = (0.48 - 1) * 100\% \]`

`\[ r = (-0.52) * 100\% \]`

`\[ r = -52\% \]`

So, the percent rate of change is
`\(-52\%\)`. Note that the negative sign indicates decay.