Question

Describe the measures of the arcs of each circle separated by the given inscribed figure. Show your work. 9. equilateral triangle ABC 10. isosceles triangle FGH, m/H = 90°

​

Answer 1

9. Equilateral triangle arcs:
`Each is \( (1)/(3) \) of circle circumference`.

10. Isosceles triangle FGH with
`\( \angle H = 90^\circ \):`
`\( (1)/(2) \)` of circle circumference.

9. Equilateral Triangle ABC:

In a circle with an inscribed equilateral triangle, each angle of the equilateral triangle subtends an arc that is one-third of the circumference. This is because an equilateral triangle has all its angles equal to 60 degrees, and in a circle, an angle subtended by an arc is proportional to the length of that arc.

So, each arc corresponding to the angles of the equilateral triangle ABC is
`\( (1)/(3) \)` of the entire circumference of the circle. If we denote the circumference of the circle as C , then the measure of each arc is
`\( (1)/(3) * C \).`

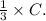
10. Isosceles Triangle FGH, ∠H = 90°:

In a circle with an inscribed isosceles triangle where one of the angles is a right angle, the measure of the arc subtended by the right angle is equal to half of the circumference of the circle. This is because a right angle subtends a semicircle.

So, for the isosceles triangle FGH with
`\( \angle H = 90^\circ \),` the measure of the arc corresponding to
`\( \angle H \) is \( (1)/(2) \)` of the circumference of the circle. If we denote the circumference as C, then the measure of the arc is
`\( (1)/(2) * C \).`

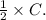
In both cases, the relationship between the angle measure and the arc measure is based on the fact that the angle subtended by an arc in a circle is proportional to the length of that arc.