Question

In ADEF, sin D = 24. What is cos E?

O A. 10/24
O B. 10/26
O C. 26/10
O D. 24/26

Answer 1

`\(\cos E = (24)/(26)\)`

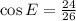
It looks like there might be some confusion in your explanation. Let me clarify the steps for finding cos E in the given context.

Given that cos E = 10/26, and you want to find the length of EF in triangle ADEF using the trigonometric ratio sine (sin), you can follow these steps:

1. Start with the trigonometric identity:

`\[ \sin^2 E + \cos^2 E = 1 \]`

2. Substitute the given value of cos E into the equation:

`\[ \sin^2 E + \left((10)/(26)\right)^2 = 1 \]`

3. Solve for
`\(\sin E\)`:

`\[ \sin^2 E + (100)/(676) = 1 \]`

`\[ \sin^2 E = 1 - (100)/(676) \]`

`\[ \sin^2 E = (576)/(676) \]`

4. Take the square root of both sides to find cos E:

`\[ \cos E = (√(576))/(√(676)) \]`

`\[ \cos E = (24)/(26) \]`

So,
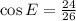`\(\cos E = (24)/(26)\)`, which is consistent with the information you provided. It seems there was an error in stating that sin D is given as 24/26, as sin D should be related to angle D, not E. If you have additional information or corrections, please provide them for further clarification.