The equation of the line is y=− 4/3 x+13.
To find the equation of the line passing through the points (6,11) and (2, 25/3), we can use the slope-intercept form of a linear equation, which is given by:
y=mx+b
The slope (m) can be calculated using the formula:
m=
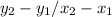
Let (x1 ,y1 )=(6,11) and (x2 ,y2)=(2, 25/3 ).
Putting values we get,
m= -1/3
Now that we have the slope, we can use one of the points (let's use (6,11)) to substitute into the equation to solve for b:
11=− 1/3(6)+b
11=−2+b
b=13
Therefore, the equation of the line is y=− 1/3x+13. To put it in slope-intercept form, we can multiply both sides by 3 to clear the fraction:
3y=−x+39
y=− 1/3x+13
So, the equation of the line passing through the given points is y=− 1/3x+13.