The answer to the question is 1.17 meters.
The triangle in the image is a right triangle, with a 64-degree angle at vertex B and a hypotenuse of 1.3 meters. We are asked to find the length of side C.
There are two ways to solve this problem: using trigonometry or using the Pythagorean theorem.
Using trigonometry:
We know that the sine of an angle is equal to the opposite side over the hypotenuse (SOH CAH TOA). In this case, the opposite side is side C and the hypotenuse is 1.3 meters. Therefore, we can write the following equation:
sin(64°) = C / 1.3 meters
Solving for C, we get:
C = 1.3 meters * sin(64°)
C ≈ 1.17 meters
Using the Pythagorean theorem:
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In this case, we can write the following equation:
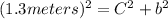
We are not given the value of side b, so we cannot solve for C using this method.
Therefore, the answer to the question is 1.17 meters.