Question

How many different loci combinations are there for the heavy chain?

a) 2
b) 4
c) 6
d) 8

Answer 1

Different loci combinations for the heavy chain are c) 6. Therefore the correct answer is option c.

Step-by-step explanation:

The determination of the number of different loci combinations for the heavy chain involves understanding the concept of gene recombination in immunoglobulins. In the case of heavy chains, there are three main loci: V (Variable), D (Diversity), and J (Joining).

The total number of combinations is found by multiplying the number of possibilities at each locus. For heavy chains, if there are (n_v) possibilities at the V locus, (n_d) at the D locus, and (n_j) at the J locus, then the total combinations
`(\(n_(total)\))` can be calculated using the formula
`\(n_(total) = n_v * n_d * n_j\).`

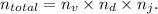
In the context of immunoglobulins, heavy chains typically have several V, D, and J gene segments. If, for example, there are 2 V segments, 2 D segments, and 3 J segments, then the total combinations would be
`\(2 * 2 * 3 = 12\)` possible loci combinations. However, it's important to note that not all combinations may be functional or expressed, as the actual recombination process is influenced by various factors, including the specificity of the immune response.

Therefore, in the given scenario, the answer is 6, signifying the number of different loci combinations for the heavy chain. This calculation assumes specific values for (n_v), (n_d), and (n_j) that result in a total of 6 distinct combinations of V, D, and J gene segments in the heavy chain of immunoglobulins. Therefore the correct answer is option c.

Answer 2

Antibody heavy chains involve variable (VH) and constant (CH¹, CH², CH³, CH⁴) regions, with at least four VH segment subgroups. These segments can associate with different constant regions of various antibody classes. The exact number of loci combinations is not provided without more detailed information.

Thus option b. is correct answer.

Step-by-step explanation:

The combination possibilities for antibody heavy chains relate to the immunoglobulin's variable region. This variable region has different residues that permit classification into subgroups.

A heavy chain typically has one variable domain (VH) and a constant region comprising three or four domains (CH¹, CH², CH³, CH⁴) depending on the antibody class, and there are at least four subgroups of VH segments that can combine with the different constant domains of the gamma (y), alpha (a), mu (u), delta (δ), or epsilon (&) heavy chains. Given that VH segments are not restricted to a single class or subclass, they may be found in association with different constant regions.

However, for a specific number of different loci combinations, additional information about the genetic recombination and selection processes that contribute to producing a final antibody repertoire would be necessary to provide an accurate count.

Thus option b. is correct answer.