Question

Leo designs a piece of jewelry in the shape of a regular pentagon

Answer 1

So, each interior angle in Leo's designed piece of jewelry, in the shape of a regular pentagon, measures
`\( 108^\circ \).`

In a regular pentagon, all interior angles are equal. The formula to calculate the measure of each interior angle in a regular polygon is given by:

`\[ \text{Interior Angle} = ((n-2) * 180^\circ)/(n) \]`

where
`\( n \)` is the number of sides. For a regular pentagon
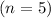`(\( n = 5 \))`, the calculation would be:

`\[ \text{Interior Angle} = ((5-2) * 180^\circ)/(5) = (3 * 180^\circ)/(5) = 108^\circ \]`

So, each interior angle in Leo's designed piece of jewelry, in the shape of a regular pentagon, measures
`\( 108^\circ \).`

The probable question maybe:

What is the measure of each interior angle in Leo's designed piece of jewelry, considering it is in the shape of a regular pentagon?