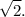The side length of a regular hexagon with area
 is
is
 . The formula for the area,
. The formula for the area,
 yields
yields

The area $A$ of a regular hexagon with side length
 can be expressed in terms of its side length using the formula:
can be expressed in terms of its side length using the formula:
![\[A = (3√(3))/(2) \cdot s^2.\]](https://img.qammunity.org/2024/formulas/mathematics/college/daezgs2yzvrr1u9grmti8ighz25n6r1tt2.png)
In this case, you are given that
 Therefore, you can set up the equation:
Therefore, you can set up the equation:
![\[3 = (3√(3))/(2) \cdot s^2.\]](https://img.qammunity.org/2024/formulas/mathematics/college/73i70nihqni2rdks5m1790dbpit9tvgl79.png)
To solve for the side length
 you can rearrange the equation:
you can rearrange the equation:
![\[s^2 = (2)/(√(3)).\]](https://img.qammunity.org/2024/formulas/mathematics/college/pl0rsu4jsbvxm4883ghh9kcdml7r8tzhsv.png)
Now, take the square root of both sides to find the side length:
![\[s = \sqrt{(2)/(√(3))}.\]](https://img.qammunity.org/2024/formulas/mathematics/college/c546p2tlu36nfs0ewdbk0zubdn23w04fs6.png)
To rationalize the denominator, multiply the numerator and denominator by the conjugate of
 :
:
![\[s = \sqrt{(2)/(√(3))} \cdot (√(3))/(√(3)) = \sqrt{(6)/(3)} = √(2).\]](https://img.qammunity.org/2024/formulas/mathematics/college/aj33eiv0akk7kmndg5yi6rm5ihf63lqdhd.png)
So, the side length of the regular hexagon is