The solution to the system of equations
 and
and
 is x = 3 and y = 5. The values satisfy both equations simultaneously, representing the intersection point on the graph.
is x = 3 and y = 5. The values satisfy both equations simultaneously, representing the intersection point on the graph.
To find the solution to the system of equations Y_1 = -x + 8 and Y_2 = 5x - 4, set the two expressions equal to each other since they represent y:
![\[\begin{align*}-Y_1 & = Y_2 \\-x + 8 & = 5x - 4\end{align*}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eenrs0ayuurle91yf23re79rtok3uytm2i.png)
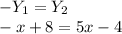
Now, solve for x:
![\[\begin{align*}4x & = 12 \\x & = 3\end{align*}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mbp0mf8wi27axugyhjqs6jx2cm74z4l1o6.png) 4x = 12
4x = 12
x = 3
Now that you have the value of x, substitute it back into either equation to find the corresponding y. Let's use
 :
:
![\[\begin{align*}Y_1 & = -x + 8 \\Y_1 & = -3 + 8 \\Y_1 & = 5\end{align*}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/l5o5v2dz0nthb9ccdce1dfdo41z2cb9g64.png)

So, the solution to the system is x = 3 and y = 5.