Question

Given and c is a real number, what is the multiplicative inverse of 0 1

Answer 1

The multiplicative inverse of 4c + 5 is
`\(-(4)/(5)\)`. This value, when multiplied by 4c + 5, yields the identity element for multiplication, which is 1.

The given equation is 4c + 5 = 0, and we need to find the multiplicative inverse of 4c + 5. The multiplicative inverse of a number is another number that, when multiplied by the original number, results in the identity element for multiplication, which is 1.

To find the multiplicative inverse, first, isolate c in the equation
4c + 5 = 0:

4c = -5

Now, divide both sides by 4 to solve for c:

`\[ c = -(5)/(4) \]`

The multiplicative inverse of 4c + 5 is the reciprocal of this value:

`\[ \text{Multiplicative Inverse} = (1)/(-(5)/(4)) = -(4)/(5) \]`

Therefore, the multiplicative inverse of
`\(4c + 5\) is \(-(4)/(5)\).`

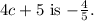
Que. Given 4c + 5 = 0 and c Is a real number what is the multiplicative inverse of 4c + 5?