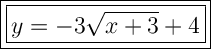Question

Pls helppppp

.
Z
A
A
A
A
A

A
Z
Z

Answer 1

`y=-3√(x+3)+4`

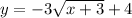
Explanation:

The given form of a square root function is:

`y = a√(x - h) + k`

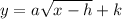
The expression under the square root sign must be non-negative for the function to be defined. Therefore, the domain is restricted to the set of values of x for which (x - h) ≥ 0, so x ≥ h.

The domain of the graphed function is x ≥ -3, so:

`h = -3`

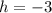
The parent square root function is y = √x. Since the domain is restricted to x ≥ 0 and the range is y ≥ 0, the graph of y = √x is a curve that starts at the origin (0, 0) and extends to the right, staying in the first quadrant.

The k-value of the general formula is equivalent to the vertical shift of the function. As the y-value of the start of the graphed function is y = 4, then:

`k = 4`

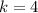
As the graphed function starts at (-3, 4) and extends to the right, moving from the second quadrant down to the fourth quadrant, the curve is a reflection in the x-axis of the parent function. Therefore, the a-value is negative.

So, the equation of the graphed function is:

`y=-a√(x+3)+4`

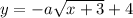
To find the value of a, we can substitute a point on the curve into the equation. Let's use (-2, 1):

`1=-a√(-2+3)+4`

`1=-a√(1)+4`

`1=-a+4`

`a=4-1`

`a=3`

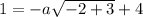
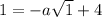
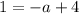
Therefore, the equation of the graphed function is:

`\Large\boxed{\boxed{y=-3√(x+3)+4}}`